Data storages: Traditional relational database management systems (RDBMS) are still the standard method for data storage. It serves as a good solution not only for querying the data, using SQL, but also for providing strong consistency. However, RDBMS systems turn out to be insufficient in many cases. They do not allow efficient storage of very large data sets and have problems ensuring adequate performance with a large number of clients simultaneously operating on these data. In recent years, software that competes with databases has been developed very actively. Currently, there are more than 200 officially recognized systems of this type, collectively called NoSQL¹. In the vast majority of cases, these systems allow you to store data in a distributed environment, enabling one to gain much greater efficiency in collecting, sharing, and processing such large data sets. Novel data stores often use multi layered architecture to achieve efficiency^2,3 which can utilize and integrate different types of memories⁴. One of the most recognizable example of such layered systems are storages based on Log-Structured Merge (LSM) trees⁵.

Data consistency issues: To effectively and reliably manage Big Data, you need not only the right hardware infrastructure but also the right software. In most cases, software solutions are preferred over hardware solutions so that NoSQL systems can work on commodity hardware⁶. However, NoSQL systems that store data in a distributed environment are also not free from flaws. One of the most severe shortcomings of these systems is the lack of strong consistency models. The vast majority of NoSQL systems do not support traditional transactions known from relational databases. There is also a group of systems that support transactions, but this support is related to the degradation of other features, according to the CAP (Consistency, Availability, Partition tolerance) theorem⁷.

Data replication issues: Consistency problems become more serious in the case of data item replication. In such a case, there is no standard way to preserve consistency⁸. Furthermore, all consistency-preserving methods can not be applied without introducing some drawbacks. Many systems that support replication decide to weaken the consistency model or prevent further data item modifications.

Background: Scalable Distributed Two-Layer Data Structures⁹ (SD2DS) is an interesting concept of a system that fits perfectly into the NoSQL concept. Although research on such systems dates back to the 1990s¹⁰, these concepts are becoming useful again thanks to the spread of cloud computing^11,12. Recent work aimed at creating an efficient data store based on SD2DS turned out to be an interesting concept¹³. It was shown that this type of storage can seriously compete with commonly available NoSQL solutions¹⁴. In the previous work of the authors, we provided a method to preserve basic consistency in SD2DS¹⁵. However, that work did not cover the consistency with replication of data items.

Goal and challenges: The architecture presented in the previous work of the authors¹⁵ did not provide replication, which seriously affects availability and throughput. Because of that in this paper, we decided to focus on providing architecture of the NoSQL system that enables greater throughput by using replication of data items in a dynamic way while still preserving strong consistency. Therefore, our goal was to propose NoSQL system with the following characteristics: (1) high availability, (2) enhanced throughput, (3) strong consistency, and (4) space scalability. The inclusion of data replication added a new layer of complexity, necessitating a reevaluation of how consistency is maintained in the proposed system. In the case of the previous SD2DS system, in the single replica situation, it was possible to properly schedule all the incoming requests. However, in the case of the proposed system in a multi-replica environment, global scheduling is not possible since each node receives only part of the requests. Because of that, a new way of dealing with consistency is required.

Contributions: Our main contributions in this paper are the following:

1. (1)

   We identified and analyzed the inconsistencies in the case of SD2DS architecture with increased throughput in the case of concurrent operations execution as well as in the case of unfinished operations,

2. (2)

   We proposed mechanisms of preserving consistency with increased throughout dedicated for SD2DS,

3. (3)

   We proved the theoretical correctness of the proposed solution,

4. (4)

   We experimentally evaluated the performance of the proposed solution compared to common NoSQL systems such as MemCached and MongoDB.

Outline: This paper is organized as follows. “Related work” presents related work. “Scalable distributed two-layer data structures” describes Scalable Distributed Two-Layer Data Structures. In “Proposed approach-SD2DS with enhanced throughput” the proposed mechanisms of preserving consistency with increased throughout dedicated for SD2DS are presented. The following section shows the results of the proposed model performance evaluation compared with common NoSQL systems such as MemCached and MongoDB. The paper ends with a conclusion and future works directions.

Historically, first NoSQL systems focused primarily on performance aspects, ignoring consistency issues. This trend was driven primarily by the CAP theorem¹⁶. However, the Basic Available, Soft-state, Eventually Consisted (BASE) model¹⁷ was suitable only for a specific subset of information systems, such as social networks. The eventual consistency model (EC) assumed that all changes would be propagated to all replicas, but clients might still experience inconsistencies¹⁸. Despite the ease of implementation, this model soon became insufficient. Next, the BASE concept was driven out by models that present stronger consistency in the Basic Availability, Scalability, Instant Consistency (BASIC) model¹⁹. It usually uses a strong or causal consistency model (CC)²⁰.

Today, many highly distributed systems do not provide any consistency or even can not guarantee persistence of data items²¹. Most of the system still provides options only for strong consistency or no consistency at all without any intermediate levels²².

In addition to consistency, the important characteristic of such distributed systems is availability, which is typically achieved by using replication. This can lead to more consistency problems and require the use of an advanced coordination protocol. Primary backup replication (PBR)²³ is one of the most typical algorithms used in such situations. It is based on the conception that there exists a primary copy of the data that is responsible for distributing the changes to backup copies. On the other hand, chain replication (CR)²⁴ uses a predefined sequence of replicas that are updated sequentially.

Both the PBR and CR protocols require a predefined replica to be considered as a main copy. This fact can cause problems with respect to efficiency and fault tolerance. To deal with this issue, distributed consensus algorithms can be used. Paxos²⁵ is one of the most popular consensus protocols used in NoSQL systems. Apart from advantages such as tolerating faults of participants, Paxos is known for its coordination overhead²⁶ because it requires additional messages to elect the leader, complete the consensus, etc. Due to this, the consensus protocol is mostly used to ensure a consistent system configuration and was only recently utilized to preserve the consistency of the data item level²⁷.

Table 1 summarizes the existing replication and consistency methods and its impact on fault tolerance, coordination overhead and latency. In case of the coordination overhead Paxos algorithm requires the most messages which can seriously affect latency. On the other hand, Paxos offers better fault tolerance than other options. The lowest level of fault tolerance is represented by CR protocol. It is caused by the fact that the fault in each participant will break the chain and prevent completion of the change. On the other hand, lowest latency can be achieved for the EC model.

There is an active development in the area of the replication algorithms. A good overview of such protocols can be found in⁸. Unfortunately, the vast majority of those protocols seriously affect consistency issues or are not developed to preserve consistency at all. Despite typical features that may apply to replication algorithms, such as high availability²⁸, load balancing²⁹, and bandwidth consumption³⁰, modern algorithm also focuses on other features such as energy consumption³¹.

In²² the protocol is proposed to provide consistency especially for service-oriented applications³². It allows one to define a consistency level at the run time that is appropriate for a specific application. In³³ a consistent protocol is proposed that allows dynamically changing the number of replicas to achieve an acceptable availability level. However, this protocol is considered to have a low response time⁸. In³⁴ the consistency protocol that takes into account the levels of quality of service. Similarly, it can also be considered as a highly time complex algorithm with high bandwidth consumption⁸. In²⁶ a combination of PBR and CR is utilized to obtain unidirectional replication. However, in this protocol, consistency is achieved by applying a serious message overhead in case of a failure. In³⁵ a protocol using groups of replicas was proposed that allows one to ensure casual consistency.

All in all, the presented literature review revealed that the solutions presented in the literature have flaws and imperfections in terms of consistency, replication, and throughput. Therefore, it is advisable to undertake further work to develop specific data stores that are tailored to the certain needs.

The main idea behind SD2DS is to divide the data item (component) into two independently managed parts. The component header ((h_k)) is responsible for storing all metadata regarding the data item. The second part, the component body ((b_k)), stores the actual data. The headers and bodies of the components are stored separately in different buckets of the SD2DS structure ((W_H) and (W_B))¹⁵. The complete set of all components stored in the system is denoted as F. The separate set of header and body buckets creates two layers of SD2DS architecture. The buckets are run on physical nodes of cluster. Depending on the configuration, each hardware node can contain a single bucket, multiple buckets of the same layer, or can share buckets of the first and second layer.

The most important part of the header of the component is the component locator, which indicates the address of the body of the component. It allows one to find the required data item based on the information provided in the header of the component. However, the first layer requires some advanced distributed organization to properly address the headers. Although different techniques could be used, we found that Distributed Linear Hashing ((LH^*))¹⁰ based on a simple key (k) of an integer value is very efficient. During our research, we also investigated the methods that address our components based on the content of the data³⁶. (LH^*) requires usage of coordinator which is responsible for managing the first-layer buckets (expanding and shrinking the number of buckets) and does not play any role during the operations of clients. In the two-layered architectures the coordinator is also responsible for managing the addresses of the second-layer buckets. It provides the address that is used to create new locators of the components body. Since many bodies can be stored on single second-layer bucket the role of the coordinator in this scenario is also limited to the situation of expanding the number of buckets.

Separation of the header and bucket components allows one to ensure the high performance of our data store^13,14 and also allows one to equip it with some advanced techniques such as data anonymity³⁷ since privacy considerations of data storage are actively studied now³⁸. On the other hand, these separations introduce many inconsistency problems that were identified and fixed in¹⁵ by introducing custom scheduling algorithms.

The basic scheduling presented in¹⁵ turns out to be insufficient for architectures with higher throughput. If the body has already been duplicated, the queries go to one of the two buckets in the second layer. Therefore, scheduling each operation within a component becomes a complex task. On the other hand, body change routines must be handled by all buckets containing copies, so they can be properly ordered.

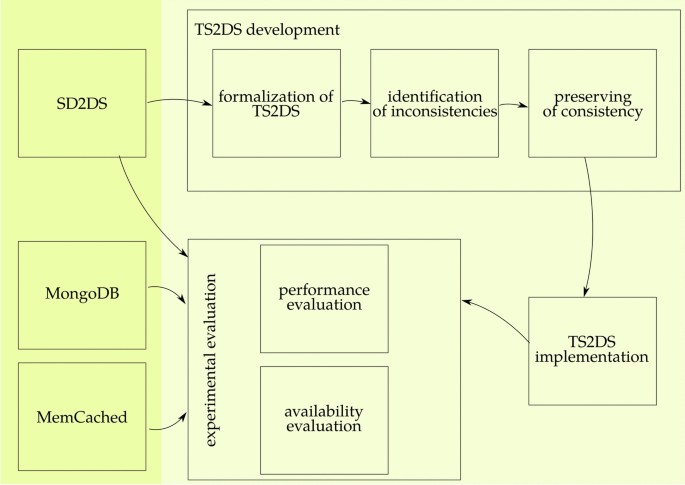
The proposed approach is presented in Fig. 1. The new architecture was developed on the basis of the SD2DS store. This step includes preparing the formal analysis of the store, identification of the inconsistencies, and providing algorithms to preserve consistency. Next, after implementation, the store was analyzed in terms of performance and availability compared to other NoSQL storages.

The flow chart of the research process. To asses the consistency level the theoretical model of TS2DS was created. This model allows to identify all the inconsistencies that could occur during TS2DS operations. Next, algorithms for preserving consistency were proposed and their theoretical correctness were presented. TS2DS implementation allows to evaluate the performance with comparison to MongoDB and MemCached.

Full size image

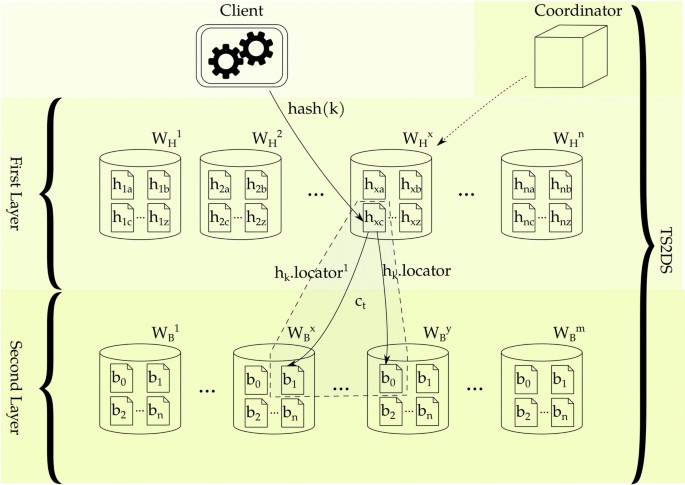
To ensure enhanced throughput in SD2DS additional copies of body are introduced in such a way that those copies are used for load balancing. In this study, we present the architecture with at most two copies of the body. This solution can be easily extended to an arbitrary number of copies. The overall architecture of SD2DS with enhanced throughput (TS2DS) is presented in Fig. 2. Each data item, stored in the TS2DS, is connected to the component. The component body stores actual data, while the component header stores additional metadata. The most important parts of the header are two locators (which point to the data bodies) and a reference counter (which counts the number of accesses to the specified component). During inserting of the component, only one body of the component is created, and reference counter is set to zero (i. e. no data replication is used). During each component retrieval, the component body is recovered based on the first locator, and the value of the reference counter is incremented. If the value of reference counter exceeds a predefined threshold, the component becomes replicated. The component body is copied, and its location is stored in the second locator. After that, component retrieval is possible from both the first and the second locations.

The architecture of TS2DS—the single component consists of the header (h) and up to two bodies (b); the headers are located in the first layer buckets ((W_H)) and the bodies are located in the second layer buckets ((W_B)); component body is accessed using locators that are essential part of the header ((h_k.locator) and (h_k.locator^1)); headers are located using hash(k) function; coordinator is used to organize first layer buckets.

Full size image

As can be seen in Fig. 2, each component contains two locators associated with it. Because of that, the component header is defined as follows:

An additional copy of the data item is located based on the second locator ((textit{locator}^1)), which is created when the reference counter (textit{rc}) exceeds the predefined value ((textit{THRESHOLD})). Most of the values in the header are immutable. The only exception is the value of (textit{rc}), which depends on time.

To provide enhanced throughput, it is vital to ensure that

In summary the main differences between the SD2DS and TS2DS are as follows: (1) the new form of the component header (consisting of second body locator); (2) the different definition of inconsistencies; (3) the new method of allocating bodies (following Eq. 2); (4) the new operation (textit{COPY}(i,k)) (required for performing component replication); (5) the new scheduling algorithm (including partial scheduling); (6) different component modification algorithm (following Eq. 3); (7) the new algorithm to check the completeness of the operation.

Formalization of operations on TS2DS

To ensure basic functionality in the data store, four primary operations were defined:

• (textit{PUT}(k,b_k))—primary operation to insert the component in the data store, presented in Algorithm 1;

• (textit{GET}(k))—primary operation to obtain the component from the data store, presented in Algorithm 2;

• (textit{DEL}(k))—primary operation to remove the component from the data store, presented in Algorithm 3;

• (textit{UPDATE}(k, b_k^prime )) – primary operation to update the component into the data store, presented in Algorithm 4.

All of those basic primary operations consist of atomic operations that are performed in sequence. The client performs the operation CH to properly find the first-layer bucket based on some function Hash(k). The operations of writing header ((Z_1)), reading header ((O_1)), deleting header ((U_1)), preparing header for copying body ((SC_1)) and performing bucket split (S) are carried out by first layer buckets. Operations of writing body ((Z_2)), writing second copy of body ((Z_3)), reading body ((O_2)), deleting body ((U_2)), deleting second copy of body ((U_3)), getting body for copying ((SC_2)) and copying body ((SC_3)) are carried out using second layer buckets. The main assumption behind these algorithms is that during the creation, only one copy of the body is used. An additional copy is created only if the component will receive a pre-defined number of requests (THRESHOLD). That means before creating new copy of the body the component is managed in the same way as in SD2DS system. The actual number of requests for each component is stored in the reference counters ((textit{rc})) in the component header.

In relation to the basic SD2DS architecture¹⁵, the TS2DS architecture introduces an additional primary operation that creates a copy of the component body (big (textit{COPY}_{textit{TS2DS}}(i,k)big )). This primary operation should follow the 5 algorithm. It consists of three operations. The (SC_1) operation is responsible for modifying the component header in such a way that it is aware of the existence of a second copy of the body. This operation uses a function to create a new locator (big (textbf{new}(b_j,h_j.textit{locator})big )), which additionally takes the number of the bucket into which a copy of the body cannot go, according to the dependence 2. The (textit{SC}_2) operation does a simple read of the body from the first location, which is used to write the second copy by the (textit{SC}_3) operation.

(textit{PUT}(k,b_k)) Inserting component into TS2DS

Full size image

(textit{GET}(k)) Getting component from TS2DS

Full size image

(textit{DEL}(k)) Deleting component from TS2DS

Full size image

(textit{UPDATE}(k, b_k^prime )) Updating component in TS2DS

Full size image

(textit{COPY}(i,k)) Copying body in TS2DS

Full size image

The (O_1) atomic operation for the (textit{UPDATE}_{textit{TS2DS}}(k, b_k^prime )) primary operation does not require additional steps to determine the locator, as is the case with (textit{GET}_{textit{TS2DS}}(k)). However, these additional steps do not affect how (textit{UPDATE}_{textit{TS2DS}}(k, b_k^prime )) works. Therefore, the same operation symbol is used in both primary operations.

Unlike the four basic routines (big (textit{PUT}_{textit{TS2DS}}(k,b_k)), (textit{GET}_{textit{TS2DS}}(k)), (textit{DEL}_{textit{TS2DS}}(k)) and (textit{UPDATE}_{textit{TS2DS}}(k, b_k^prime )big )), the additional routine (textit{COPY}_{textit{TS2DS}}(i,k)) is not initialized by the client. The appropriate bucket of the first layer containing the header of the copied component is responsible for its execution. Therefore, this primary operation does not require the (textit{CH}) operation to find the number of the first layer bucket (i) containing the header.

Identification of inconsistencies in TS2DS

Since for a single component there can exist two bodies ((b_k) and (hat{b_k})) they must be identical. In the other case, the Mismatch Body Inconsistency (MBI) arises. This inconsistency is defined below.

Definition 1

When the condition is met (displaystyle mathop {{exists }}_{k: h_k.rc > THRESHOLD} big ( b_k ne hat{b_k} wedge (h_k,b_k) in F wedge (h_k,hat{b_k}) in Fbig )), the Mismatch Body Inconsistency (MBI) arises.

In the traditional SD2DS architecture, the existence of two bodies for a single component was considered an inconsistency. However, in the case of the TS2DS, due to the additional copy of the component body, this situation is completely normal. Due to equation 2, it is important to ensure that both bodies are located in different second-layer buckets. However, due to inconsistency problems, Duplicated Body Inconsistency (DBI) may still arise when the following condition is met.

Definition 2

When the condition is met (mathop {{exists }}_{h_k in H; b_k,b_k^prime in B}) (big ( (h_k,b_k) in F wedge (h_k,b_k^prime ) in F wedge {Addr}(b_k) = {Addr}(b_k^prime ) big )), the Duplicated Body Inconsistency (DBI) arises.

Due to the two-layer architecture of TS2DS, the typical operation to retrieve a component requires access to both a header and a body of the component. In that case, the Deleted Component Inconsistency (DCI) may arise when the component header was successfully retrieved, but the corresponding component body is missing. This situation may arise during the concurrent execution of operations. Contrary to traditional SD2DS architecture, in the case of TS2DS, the need to retrieve the body of the component occurs in both the (textit{GET}(k)) and (textit{COPY}(i,k)) primary operations. Due to this, the DCI inconsistency is defined as follows.

Definition 3

Deleted Component Inconsistency (DCI) is defined as: (big (displaystyle mathop {{exists }}_{GET(k)} big ( GET(k) = CH rightarrow O_1 rightarrow O_2 big )) (wedge) (O_1: (h_k,b_k) in F) (wedge) (O_2: (h_k,b_k) notin Bbig ))

(vee)

(big (displaystyle mathop {{exists }}_{COPY(i,k)} big ( COPY(i,k) = textit{SC}_1 rightarrow textit{SC}_2 rightarrow textit{SC}_3 big )) (wedge) (textit{SC}_1: (h_k,b_k) in F) (wedge) (textit{SC}_2: (h_k,b_k) notin Bbig ))

Orphan Header Inconsistency (OHI) and Orphan Body Inconsistency (OBI) apply to TS2DS in the same way as applied to SD2DS¹⁵.

Definition 4

When the condition is met (displaystyle mathop {{exists }}_{h_i in H} displaystyle mathop {{forall }}_{b_j in B} big ( (h_i,b_j) notin F big )), the Orphan Header Inconsistency (OHI) arises.

Definition 5

When the condition is met (displaystyle mathop {{exists }}_{b_i in B} displaystyle mathop {{forall }}_{h_j in H} big ( (h_j,b_i) notin F big )) the Orphan Body Inconsistency (OBI) arises.

With a careful analysis of all possible concurrent execution of primary operations, it was possible to pinpoint all inconsistencies that were caused by extensions that provided increased throughput. Lemma 1 summarizes the occurrences of MBI inconsistencies. The occurrences of DBI inconsistencies are summarized in lemma 2. The observation 3 summarizes all the cases of inconsistencies DCI. All occurrences of inconsistencies OHI and OBI inconsistencies are summarized in Lemma 4 and 5, respectively. The sequence of operations is indicated with the (rightarrow) symbol.

Lemma 1

By introducing an additional copy of the body, assuming that all operations were completely executed during the concurrent execution of any two primary operations, MBI is critical only in the following situations.

• (textit{MBI}_1), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{UPDATE}(k, b_k^{prime prime }) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow U_2^{prime prime } rightarrow Z_2^{prime prime } rightarrow U_3^{prime prime } rightarrow Z_3^{prime prime }) the permanent MBI causes an error after (Z_3^prime) if and only if (Z_2^prime rightarrow Z_2^{prime prime }) and (Z_3^{prime prime } rightarrow Z_3^prime) when (h_k.textit{locator}^1 ne textit{NULL});

• (textit{MBI}_2), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{UPDATE}(k, b_k^{prime prime }) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow U_2^{prime prime } rightarrow Z_2^{prime prime } rightarrow U_3^{prime prime } rightarrow Z_3^{prime prime }) the permanent MBI causes an error after (Z_3^{prime prime }) if and only if (Z_2^{prime prime } rightarrow Z_2^prime) and (Z_3^prime rightarrow Z_3^{prime prime }) when (h_k.textit{locator}^1 ne textit{NULL});

• (textit{MBI}_3), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the permanent MBI causes an error after (textit{SC}_3^{prime prime }) if and only if (O_1^prime rightarrow textit{SC}_1^{prime prime }) and (textit{SC}_2^{prime prime } rightarrow Z_2^prime) when (h_k.textit{locator}^1 = textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD});

• (textit{MBI}_4), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the permanent MBI causes an error after (textit{SC}_3^{prime prime }) if and only if (textit{SC}_1^{prime prime } rightarrow O_1^prime) and (textit{SC}_2^{prime prime } rightarrow Z_2^prime) and (Z_3^prime rightarrow textit{SC}_3^{prime prime }) when (h_k.textit{locator}^1 = textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD}).

Lemma 2

By introducing an additional copy of the body, assuming that all operations were completely executed during the concurrent execution of any two primary operations, DBI is critical only in the following situations.

• (textit{DBI}_1), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{UPDATE}(k, b_k^{prime prime }) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow U_2^{prime prime } rightarrow Z_2^{prime prime } rightarrow U_3^{prime prime } rightarrow Z_3^{prime prime }) the permanent DBI causes an error after (Z_3) operations if and only if (U_3^prime rightarrow Z_3^{prime prime }) i (U_3^{prime prime } rightarrow Z_3^prime) when (h_k.textit{locator}^1 ne textit{NULL});

• (textit{DBI}_2), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the permanent DBI causes an error after (Z_3^prime) if and only if (textit{SC}_1^{prime prime } rightarrow O_1^prime) and (U_3^prime rightarrow textit{SC}_3^{prime prime } rightarrow Z_3^prime) when (h_k.textit{locator}^1 ne textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD});

• (textit{DBI}_3), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the permanent DBI causes an error after (textit{SC}_3^{prime prime }) if and only if (textit{SC}_1^{prime prime } rightarrow O_1^prime) and (Z_3^prime rightarrow textit{SC}_3^{prime prime }) when (h_k.textit{locator}^1 = textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD}).

Lemma 3

By introducing an additional copy of the body, assuming that all operations were completely executed during the concurrent execution of any two primary operations, DCI is critical only in the following situations.

• (textit{DCI}_1), during concurrent execution of (textit{PUT}(k, b_k) = textit{CH}_1^{prime } rightarrow Z_1^{prime } rightarrow Z_2^{prime } rightarrow S^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the DCI causes an error in (textit{SC}_2^{prime prime }) if and only if (Z_1^prime rightarrow textit{SC}_1^{prime prime }) and (textit{SC}_2^{prime prime } rightarrow Z_2^prime) when (h_k.textit{locator}^1 = textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD});

• (textit{DCI}_2), during concurrent execution of (textit{DEL}(k) = textit{CH}_1^{prime } rightarrow U_1^{prime } rightarrow U_2^{prime } rightarrow U_3^{prime }) and (textit{GET}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow O_2^{prime prime }) the DCI causes an error in (O_2^{prime prime }) if and only if (O_1^{prime prime } rightarrow U_1^prime) and (U_2^prime rightarrow O_2^{prime prime }) when (h_k.textit{locator}^1 ne textit{NULL}) and (h_k.textit{rc} bmod 2 = 0);

• (textit{DCI}_3), during concurrent execution of (textit{DEL}(k) = textit{CH}_1^{prime } rightarrow U_1^{prime } rightarrow U_2^{prime } rightarrow U_3^{prime }) and (textit{GET}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow O_2^{prime prime }) the DCI causes an error in (O_2^{prime prime }) if and only if (O_1^{prime prime } rightarrow U_1^prime) and (U_3^prime rightarrow O_2^{prime prime }) when (h_k.textit{locator}^1 ne textit{NULL}) and (h_k.textit{rc} bmod 2 = 1);

• (textit{DCI}_4), during concurrent execution of (textit{DEL}(k) = textit{CH}_1^{prime } rightarrow U_1^{prime } rightarrow U_2^{prime } rightarrow U_3^{prime }) and (textit{COPY}(i,k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the DCI causes an error in (textit{SC}_2^{prime prime }) if and only if (textit{SC}_1^{prime prime } rightarrow U_1^prime) and (U_2^prime rightarrow textit{SC}_2^{prime prime }) when (h_k.textit{locator}^1 = textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD});

• (textit{DCI}_5), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{GET}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow O_2^{prime prime }) the DCI causes an error in (O_2^{prime prime }) if and only if (U_2^prime rightarrow O_2^{prime prime } rightarrow Z_2^prime) when (h_k.textit{locator}^1 ne textit{NULL}) and (h_k.textit{rc} bmod 2 = 0);

• (textit{DCI}_6), during concurrent execution of (textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{GET}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow O_2^{prime prime }) the DCI causes an error in (O_2^{prime prime }) if and only if (U_3^prime rightarrow O_2^{prime prime } rightarrow Z_3^prime) when (h_k.textit{locator}^1 ne textit{NULL}) and (h_k.textit{rc} bmod 2 = 1);

• (textit{DCI}_7), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the DCI causes an error in (textit{SC}_2^{prime prime }) if and only if (U_2^prime rightarrow textit{SC}_2^{prime prime } rightarrow Z_2^prime) when (h_k.textit{locator}^1 = textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD});

• (textit{DCI}_8), during concurrent execution of (textit{COPY}(i,k) = textit{SC}_1^{prime } rightarrow textit{SC}_2^{prime } rightarrow textit{SC}_3^{prime }) and (textit{GET}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow O_2^{prime prime }) the DCI causes an error in (O_2^{prime prime }) if and only if (textit{SC}_1^prime rightarrow O_1^{prime prime }) and (O_2^{prime prime } rightarrow textit{SC}_3^prime) when (h_k.textit{locator}^1 ne textit{NULL}) and (h_k.textit{rc} bmod 2 = 1).

Lemma 4

By introducing an additional copy of the body, assuming that all operations were completely executed during the concurrent execution of any two primary operations, OHI is critical only in the following situations.

• (textit{OHI}_1), during concurrent execution of (textit{PUT}(k, b_k) = textit{CH}_1^{prime } rightarrow Z_1^{prime } rightarrow Z_2^{prime } rightarrow S^{prime }) and (textit{COPY}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow U_2^{prime prime } rightarrow Z_2^{prime prime } rightarrow U_3^{prime prime } rightarrow Z_3^{prime prime }) the transient OHI causes an error in (SC_2^{prime prime }) if and only if (Z_1^prime rightarrow textit{SC}_1^{prime prime }) and (textit{SC}_2^{prime prime } rightarrow Z_2^prime), when (h_k.textit{locator}^1 = textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD}) and (textit{THRESHOLD} = 0);

• (textit{OHI}_2), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{GET}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow O_2^{prime prime }) the transient OHI causes an error in (O_2^{prime prime }) if and only if (U_2^prime rightarrow O_2^{prime prime } rightarrow Z_2^prime) when (h_k.textit{locator}^1 ne textit{NULL}) and (h_k.textit{rc} bmod 2 = 0)

• (textit{OHI}_3), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{GET}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow O_2^{prime prime }) the transient OHI causes an error in (O_2^{prime prime }) if and only if (U_3^prime rightarrow O_2^{prime prime } rightarrow Z_3^prime) when (h_k.textit{locator}^1 ne textit{NULL}) and (h_k.textit{rc} bmod 2 = 1)

• (textit{OHI}_4), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{UPDATE}(k, b_k^{prime prime }) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow U_2^{prime prime } rightarrow Z_2^{prime prime } rightarrow U_3^{prime prime } rightarrow Z_3^{prime prime }) the transient OHI causes an error in (U_3^{prime prime }) if and only if (U_3^prime rightarrow Z_3^{prime prime }) i (U_3^{prime prime } rightarrow Z_3^prime) when (h_h.textit{locator}^1 ne textit{NULL});

• (textit{OHI}_{5}), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the transient OHI causes an error in (textit{SC}_2^{prime prime }) if and only if (U_2^prime rightarrow textit{SC}_2^{prime prime } rightarrow Z_2^prime) when (h_k.textit{locator}^1 = NULL) i (h_k.textit{rc} ge textit{THRESHOLD});

• (textit{OHI}_{6}), during concurrent execution of(textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime } rightarrow O_1^{prime } rightarrow U_2^{prime } rightarrow Z_2^{prime } rightarrow U_3^{prime } rightarrow Z_3^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the transient OHI causes an error in (U_3^prime) if and only if (textit{SC}_1^{prime prime } rightarrow O_1^prime) i (U_3^prime rightarrow textit{SC}_3^{prime prime } rightarrow Z_3^prime) when (h_k.textit{locator}^1 = textit{NULL}) i (h_k.textit{rc} ge textit{THRESHOLD});

• (textit{OHI}_{7}), during concurrent execution of (textit{COPY}(i,k) = textit{SC}_1^{prime } rightarrow textit{SC}_2^{prime } rightarrow textit{SC}_3^{prime }) and (textit{GET}(k) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow O_2^{prime prime }) the transient OHI causes an error in (O_2^{prime prime }) if and only if (textit{SC}_1^prime rightarrow O_1^{prime prime }) i (O_2^{prime prime } rightarrow textit{SC}_3^prime) when (h_k.textit{locator}^1 ne textit{NULL}) i (h_k.textit{rc} bmod 2 = 1).

Lemma 5

By introducing an additional copy of the body, assuming that all operations were completely executed during the concurrent execution of any two primary operations, the OBI is critical only in the following situations.

• (textit{OBI}_1), during concurrent execution of (textit{DEL}(k) = textit{CH}_1^{prime } rightarrow U_1^{prime } rightarrow U_2^{prime } rightarrow U_3^{prime }) and (textit{UPDATE}(k, b_k^prime ) = textit{CH}_1^{prime prime } rightarrow O_1^{prime prime } rightarrow U_2^{prime prime } rightarrow Z_2^{prime prime } rightarrow U_3^{prime prime } rightarrow Z_3^{prime prime }) the permanent OBI causes an error in (Z_3^{prime prime }) if and only if (O_1^{prime prime } rightarrow U_1^prime) i (U_3^prime rightarrow Z_3^{prime prime }) when (h_k.textit{locator}^1 ne textit{NULL});

• (textit{OBI}_2), during the concurrent execution of (textit{DEL}(k) = textit{CH}_1^{prime } rightarrow U_1^{prime } rightarrow U_2^{prime } rightarrow U_3^{prime }) and (textit{COPY}(k) = textit{SC}_1^{prime prime } rightarrow textit{SC}_2^{prime prime } rightarrow textit{SC}_3^{prime prime }) the permanent OBI causes an error in (textit{SC}_3^{prime prime }) if and only if (textit{SC}_1^{prime prime } rightarrow U_1^prime) i (U_1^prime rightarrow textit{SC}_3^{prime prime }) when (h_k.textit{locator}^1 = textit{NULL}) and (h_k.textit{rc} ge textit{THRESHOLD}).

Preserving consistency in TS2DS

Providing strong consistency between first and second layers with additional copy of the body may be preserved using a specially developed scheduling algorithm. Like what was presented in¹⁵ to perform this scheduling, a sequence number must be assigned to all operations performed on a designated component. Since each component header is managed by only one first-layer bucket, it is possible to generate those sequence numbers in a unique and monotonic fashion. The algorithm 6 presents the method to generate such numbers. For proper order of the operations, two values are used: Sequence Number of all operations (SN) and Sequence Number of the last modification (SNM). Introducing the SNM number allows scheduling non mutable operations in any way as long as all previous mutable operations were completed. It is worth to stress that both SN and SNM are local to each of the components. Because of that, their values are only managed in the buckets that are responsible for the desired component.

Generation of sequence numbers in the first layer of SD2DS: (SEQ(k,omega )).

Full size image

The algorithm 7 presents the process of scheduling operations in the second-layer buckets. The main idea behind this algorithm is to allow us to execute the operation only if the sequence number of the last modification in the second layer bucket ((SNM_B)) is the same as in the first layer ((SNM_H)). All requests that their sequence number is greater than (SNM_B) must be rejected and should be re-tried after the missing mutable operation is executed. On the other hand, a smaller sequence number is considered erroneous, since it should not be generated by the first layer.

Scheduling in the second layer of TS2DS

Full size image

The impact of using sequence number generations and scheduling on identified inconsistencies is presented in Theorem 1. As can be seen, all inconsistencies caused by the existence of the second copy of the body can be eliminated.

Theorem 1

Let (omega ^prime , omega ^{prime prime } in Omega) be the primary operations that will be executed on (c_k), and (SEQ(k, omega ^prime )= SN_H^{prime k}), (SEQ(k, omega ^{prime prime })= SN_H^{prime prime k}). All critical situations caused by (textit{OHI}), (textit{OBI}), (textit{DBI}), (textit{DCI}), and (textit{MBI}) will be eliminated if the operations are completed and scheduled using Algorithm 7.

Proof

According to the Lemma 1(textit{MBI}) inconsistencies may cause four critical situations (textit{MBI}_1)–(textit{MBI}_4):

• Assume that (omega ^prime =UPDATE(k, b_k^prime )) and (omega ^{prime prime }=)(UPDATE(k, b_k^prime )). If (Z_2^{prime } rightarrow Z_2^{prime prime }) then (SN_H^{prime k} < SN_H^{prime prime k}), therefore, according to Algorithm 7 (Z_3^{prime } rightarrow Z_3^{prime prime }), this means that (textit{MBI}_1) will never occur.

• Assume that (omega ^prime =UPDATE(k, b_k^prime )) and (omega ^{prime prime }=)(UPDATE(k, b_k^prime )). If (Z_2^{prime prime } rightarrow Z_2^{prime }) then (SN_H^{prime prime k} < SN_H^{prime k}), therefore, according to Algorithm 7 (Z_3^{prime prime } rightarrow Z_3^{prime }), this means that (textit{MBI}_2) will never occur.

• Assume that (omega ^prime =UPDATE(k, b_k^prime )) and (omega ^{prime prime }=)COPY(k). If (O_1^{prime } rightarrow textit{SC}_1^{prime prime }) then (SN_H^{prime k} < SN_H^{prime prime k}),therefore, according to Algorithm 7 (Z_2^{prime } rightarrow textit{SC}_2^{prime prime }), this means that (textit{MBI}_3) will never occur.

• Assume that (omega ^prime =UPDATE(k, b_k^prime )) and (omega ^{prime prime }=)COPY(k). If (textit{SC}_1^{prime prime } rightarrow O_1^{prime }) then (SN_H^{prime prime k} < SN_H^{prime k}), therefore according to Algorithm 7 (textit{SC}_3^{prime prime } rightarrow Z_3^{prime }), this means that (textit{MBI}_4) will never occur.

Therefore, the above analysis shows that Algorithm 7 eliminates all critical situations that can be caused by (textit{MBI}) inconsistencies. Similarly, we may prove that Algorithm 7 eliminates all critical situations identified in Lemma 2-5, i.e., that in all cases the only possible orders of execution will be the following:

• (textit{DBI}_1), if (U_3^prime rightarrow Z_3^{prime prime }) then (Z_3^prime rightarrow U_3^{prime prime });

• (textit{DBI}_2), if (textit{SC}_1^{prime prime } rightarrow O_1^prime) then (textit{SC}_3^{prime prime } rightarrow U_3^prime rightarrow Z_3^prime);

• (textit{DBI}_3), if (textit{SC}_1^{prime prime } rightarrow O_1^prime) then (textit{SC}_3^{prime prime } rightarrow Z_3^prime);

• (textit{DCI}_1), if (Z_1^prime rightarrow textit{SC}_1^{prime prime }) then (Z_2^prime rightarrow textit{SC}_2^{prime prime });

• (textit{DCI}_2), if (O_1^{prime prime } rightarrow U_1^prime) then (O_2^{prime prime } rightarrow U_2^prime);

• (textit{DCI}_3), if (O_1^{prime prime } rightarrow U_1^prime) then (O_2^{prime prime } rightarrow U_3^prime);

• (textit{DCI}_4), if (textit{SC}_1^{prime prime } rightarrow U_1^prime) then (SC_2^{prime prime } rightarrow U_2^prime);

• (textit{DCI}_5), then (U_2^prime rightarrow Z_2^prime rightarrow O_2^{prime prime }) or (O_2^{prime prime } rightarrow U_2^prime rightarrow Z_2^prime);

• (textit{DCI}_6), then (U_3^prime rightarrow Z_3^prime rightarrow O_2^{prime prime }) or (O_2^{prime prime } rightarrow U_3^prime rightarrow Z_3^prime);

• (textit{DCI}_7), then (U_2^prime rightarrow Z_2^prime rightarrow textit{SC}_2^{prime prime }) or (textit{SC}_2^{prime prime } rightarrow U_2^prime rightarrow Z_2^prime);

• (textit{DCI}_8), if (textit{SC}_1^prime rightarrow O_1^{prime prime }) then (textit{SC}_3^prime rightarrow O_2^{prime prime });

• (textit{OHI}_1), if (Z_1^prime rightarrow textit{SC}_1^{prime prime }) then (Z_2^prime rightarrow textit{SC}_2^{prime prime });

• (textit{OHI}_2), if (U_2^prime rightarrow O_2^{prime prime }) then (textit{GET}(k)) will be rejected or if (O_2^{prime prime } rightarrow U_2^prime) then (O_2^{prime prime } rightarrow U_2^prime rightarrow Z_2^prime);

• (textit{OHI}_3), if (U_3^prime rightarrow O_2^{prime prime }) then (textit{GET}(k)) will be rejected or if (O_2^{prime prime } rightarrow U_3^prime) then (O_2^{prime prime } rightarrow U_3^prime rightarrow Z_3^prime);

• (textit{OHI}_4), if (U_3^prime rightarrow Z_3^{prime prime }) then (Z_3^prime rightarrow U_3^{prime prime });

• (textit{OHI}_5) then (U_2^prime rightarrow Z_2^prime rightarrow SC_2^{prime prime }) or (textit{SC}_2^{prime prime } rightarrow U_2^prime rightarrow Z_2^prime);

• (textit{OHI}_6), if (textit{SC}_1^{prime prime } rightarrow O_1^prime) then (textit{SC}_3^{prime prime } rightarrow U_3^prime rightarrow Z_3^prime);

• (textit{OHI}_7), if (textit{SC}_1^prime rightarrow O_1^{prime prime }) and (O_2^{prime prime } rightarrow textit{SC}_3^prime) then (textit{GET}(k)) will be rejected;

• (textit{OBI}_1), if (O_1^{prime prime } rightarrow U_1^prime) then (Z_3^{prime prime } rightarrow U_3^prime);

• (textit{OBI}_2), if (textit{SC}_1^{prime prime } rightarrow U_1^prime) then (textit{SC}_3^{prime prime } rightarrow U_3^prime).

Therefore, the algorithm 7 eliminates all inconsistencies in TS2DS caused by concurrent executions of primary operations. (square)

Apart from problems caused by concurrent execution of primary operations, there might also be some problems with unfinished operations. These problems can be very serious because they could affect the work of the algorithm 7. Ensuring proper operation of the system in the event of incomplete primary operation requires the implementation of recovery methods similar to those presented in¹⁵. It turned out that it was necessary to change the way the component modification primary operation works. The sequence of atomic operations in the modifying primary operation has been modified to the following form.

The use of scheduling as in the algorithm 7 will ensure the correct operation of (textit{UPDATE}_{textit{TS2DS}}(k,b_k^prime )) with the change 3. However, this change will allow not only to withdraw but also to complete the primary operations correctly in a simple way. Lemma 6 summarize the inconsistencies that may arise from incomplete primary operations. The ({rightarrow !!!!!!!!|,,,,}) operator indicates that the execution of the primary operation is interrupted, so all atomic operations on the right-hand side will not be executed.

Lemma 6

By introducing an additional copy of the body in case of uncompleted operations, the inconsistencies arise only in the following situations.

• (textit{END}_1), during unfinished (textit{DEL}(k)) primary operation, the OBI arise if and only if (textit{CH} rightarrow U_1 rightarrow U_2 {rightarrow !!!!!!!!|,,,,}U_3) when (h_k.textit{locator} ne textit{NULL});

• (textit{END}_2), during unfinished (textit{UPDATE}^prime (k,b_k^prime )) primary operation, the MBI arise if and only if ({CH} rightarrow O_1 rightarrow Z_2 rightarrow U_2 {rightarrow !!!!!!!!|,,,,,,}Z_3 rightarrow U_3) when (h_k.textit{locator}^1 ne textit{NULL});

• (textit{END}_3), during unfinished (textit{UPDATE}^prime (k,b_k^prime )) primary operation, the DBI arise if and only if (textit{CH} rightarrow O_1 rightarrow Z_2 rightarrow U_2 rightarrow Z_3 {rightarrow !!!!!!!!|,,,,}U_3) when (h_k.textit{locator}^1 ne textit{NULL});

• (textit{END}_4), during unfinished (textit{COPY}(k,b_k)) primary operation, the OHI arise if and only if (textit{SC}_1 {rightarrow !!!!!!!!|,,,,}textit{SC}_2 rightarrow textit{SC}_3);

• (textit{END}_5), during unfinished (textit{COPY}(k)) primary operation, the OHI arise if and only if (textit{SC}_1 rightarrow textit{SC}_2 {rightarrow !!!!!!!!|,,,,}textit{SC}_3).

Due to these assumptions, it became possible to develop the algorithm 8 to ensure a consistent state of the data store in the presence of unfinished primary operations. The main idea behind this algorithm is to check whenever the appropriate atomic operation in the second bucket is performed after the atomic operation in the first layer has been executed. Also, since (textit{COPY}_{textit{TS2DS}}(i,k)) is also a body change operation, a check is made to see if it was fully executed. Since the body of the component is located in two buckets, it was necessary to enter two values (textit{SNM}_B^k), for the bucket containing the body (b_k) ((textit{SNM}_{textit{B0}}^k) ) and for the bucket containing the body (hat{b_k}) ((textit{SNM}_{textit{B1}}^k)).

The Algorithm 8 can be used together with the Algorithm 7. Using both in the system allows us to provide not only accepted level of consistency but also accepted level of fault tolerance. Algorithm 8 allows us to provide consistency not only in the faulty client environment but also during bucket faults.

The impact on the state of the system is summarized in Theorem 2. As can be seen, the use of Algorithm 8 allows one to eliminate all inconsistencies caused by unfinished primary operations.

Checking the completeness of the TS2DS operations : (textit{CHECK}(k, textit{ns}, p in P))

Full size image

Theorem 2

Let (omega ^prime in Omega) be the primary operation that will be executed on (c_k) and (SEQ(k, omega ^prime )= SN_H^{prime k}). All critical situations caused by inconsistencies (textit{END}) will be eliminated if operations are checked using the Algorithm 8.

Proof

According to Lemma 6 inconsistencies may cause five critical situations (textit{END}_1) – (textit{END}_5):

• Assume that (omega ^prime =textit{DEL}(k)). If (textit{CH} rightarrow U_1 rightarrow U_2 {rightarrow !!!!!!!!|,,,,}U_3) and (h_k.textit{locator}^1 ne textit{NULL}), then (SN_{B1}^{prime k} < SN_H^{prime k}), therefore, according to Algorithm 8, an additional operation (U_3) will be executed on (W_B^{textit{Addr}(h_j.textit{locator}^1)}), which means that (textit{END}_1) will never occur;

• Assume that (omega ^prime =textit{UPDATE}^prime (k,b_k^prime )). If (textit{CH} rightarrow O_1 rightarrow Z_2 rightarrow U_2 {rightarrow !!!!!!!!|,,,,}Z_3 rightarrow U_3) and (h_k.textit{locator}^1 ne textit{NULL}), then (SN_{B1}^{prime k} < SN_H^{prime k}), therefore, according to Algorithm 8, additional (O_2) will be executed on (W_B^{textit{Addr}(h_j.textit{locator})}) and (Z_3) and (U_3) on (W_B^{textit{Addr}(h_j.textit{locator}^1)}), which means that (textit{END}_2) will never occur;

• Assume that (omega ^prime =textit{UPDATE}^prime (k,b_k^prime )). If (textit{CH} rightarrow O_1 rightarrow Z_2 rightarrow U_2 rightarrow Z_3 mathrel {rightarrow !!!!!!!!|,,,,}U_3) and (h_k.textit{locator}^1 ne textit{NULL}), then (SN_{B1}^{prime k} < SN_H^{prime k}), therefore, according to Algorithm 8, an additional (U_3) will be executed on (W_B^{textit{Addr}(h_j.textit{locator}^1)}), which means that (textit{END}_3) will never occur;

• Assume that (omega ^prime =textit{COPY}(i,k)). If (textit{SC}_1 mathrel {rightarrow !!!!!!!!|,,,,}textit{SC}_2 rightarrow textit{SC}_3) then (SN_{B1}^{prime k} < SN_H^{prime k}), therefore, according to Algorithm 8, additional (textit{SC}_2) will be executed on (W_B^{textit{Addr}(h_j.textit{locator})}) and (textit{SC}_3) on (W_B^{textit{Addr}(h_j.textit{locator}^1)}), which means that (textit{END}_4) will never occur;

• Assume that (omega ^prime =textit{COPY}(i,k)). If (textit{SC}_1 rightarrow textit{SC}_2 mathrel {rightarrow !!!!!!!!|,,,,}textit{SC}_3) then (SN_{B1}^{prime k} < SN_H^{prime k}), therefore, according to Algorithm 8, additional (textit{SC}_2) will be executed on (W_B^{textit{Addr}(h_j.textit{locator})}) and (textit{SC}_3) on (W_B^{textit{Addr}(h_j.textit{locator}^1)}), which means that (textit{END}_5) will never occur.

(square)

We conducted a theoretical analysis of the complexity of the TS2DS operations that allows us to compare it with the well-known consensus protocol. As a comparison case, we considered a TS2DS system that uses the Paxos²⁵ protocol to maintain consistency. We use Paxos due to its popularity and applicability.

In our analysis, we adopted (T_1) as a cost of sending the message between the client and the first layer of the system. Analogously, (T_2) is the cost of sending the message from and to the second layer of the system. Since the second layer consists of the body of the component the relation following relation applies: (T_2>> T_1). The number of the body replicas is denoted as N.

In case of PUT primary operation, the TS2DS mechanism assumes realization in time (T_1+T_2). In order to achieve N replicas, an additional (N-1) COPY primary operation must be performed. Each COPY is executed in the time of (T_1+2T_2). So, the overall cost of creating N body replicas requires (NT_1+(2N+1)T_2).

In case of using Paxos to insert N copies of the component body, one needs to perform the protocol on N participants. The protocol consists of four stages. The first stage allows us to prepare the participants to create consensus. This will be executed in the time of (T_1). In the next stage, participants respond with the promise to not accept older requests. This is usually done in time (T_1). In the pessimistic case, participants need to also send the value that they already promised to accept. In such a case, this stage will take place in time (T_1+T_2). The proposal of the new value will be performed in time (T_2). The last stage of accepting the proposed value will be executed in time (T_1). Additional communication is required to apply the information to the first layer of the TS2DS. Because of that, in the optimistic case, the whole operation will be performed in the time of ((3N+1)T_1+NT_2). In the pessimistic case, it will be performed in the time of ((3N+1)T_1+2NT_2).

Other cases can be described in a similar way and are summarized in the Table 2.

To evaluate the performance of the TS2DS architecture, we performed experiments in a distributed environment. Most of the experiments used 17 servers to run buckets on them. A first-layer bucket and the second-layer bucket were launched on each server. Another server was used to run the split coordinator required by the (textit{LH}^*) architecture. The clients were launched on 10 other machines. We ran up to 10 client software instances on each clients machine. All cluster nodes worked under the control of CentOS, had 16 CPU cores, 16 GiB RAM, and a hard disk with a capacity of 150 GiB. All machines were connected by an 1 GiB/s.

We evaluated the following variants of architecture:

• (SD2DS_{PS})—architecture providing strong consistency using partial scheduling¹⁵ without additional copies of body;

• (TS2DS_{PS_{1}})—architecture with one copy of the body, rejected request were not retried;

• (TS2DS_{PS_{infty }})—architecture with one copy of the body, rejected requests were repeated until success.

Contrary to the classic (SD2DS_{PS}) architecture consistent TS2DS architectures may reject some requests if the consistent state can not be ensured. Because of that, we evaluated TS2DS architectures with two variants. In the first case, requests were canceled after one rejection attempt. In the second case, requests were repeated until successfully handled. There was no limit with respect to the number of attempts. Because of that, the second variant generates a lot of additional workload.

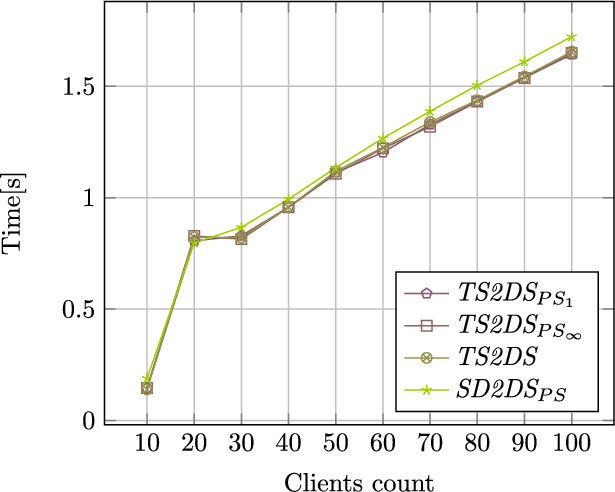
The advantages of an architecture with increased throughput become apparent when the buckets are heavily loaded with customer requests. Figure 3 shows a comparison of the throughput of individual architecture versions during a heavy load of client queries. The experiments were carried out using 256 components of 10 MiB size. We chose relatively small number of components in this particular test purposely. It allows us to generate high throughput with 100 clients. The test can be easily scaled using more components located on more buckets.

As the analysis of Fig. 3 shows, the differences between the classic architecture and the architecture with increased throughput become visible with increasing number of clients. Differences in client handling times become particularly noticeable when the number of clients exceeds the number of buckets used. Adding consistency mechanisms to the architecture with increased throughput does not result in a significant decrease in performance in the case of a large number of queries that read components. This architecture allows better performance than the classic SD2DS architecture, even after implementing mechanisms to ensure consistency.

Throughput comparison while getting components of 10 MiB.

Full size image

Performance tests were performed for situations with different proportions of clients retrieving ((C_r)) and modifying components ((C_u)). In every experiment, it was ensured that:

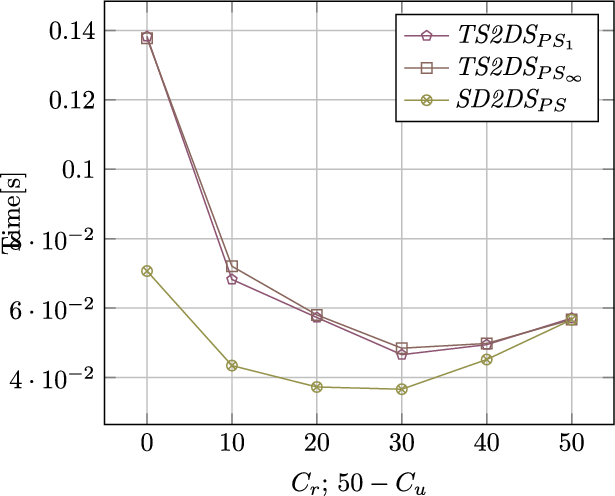
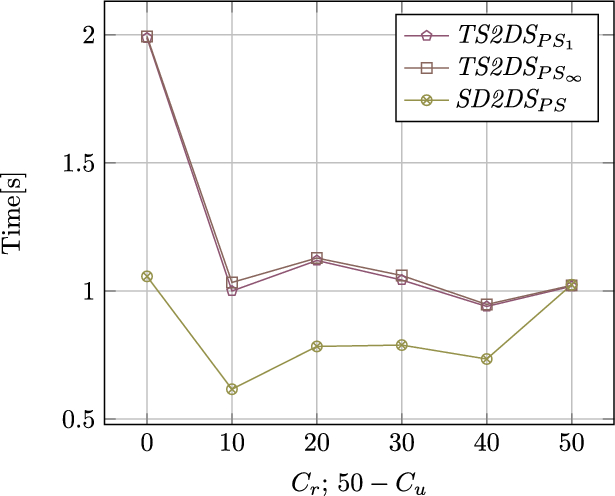
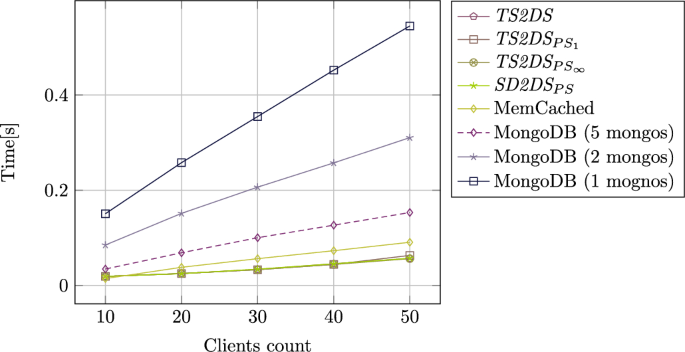
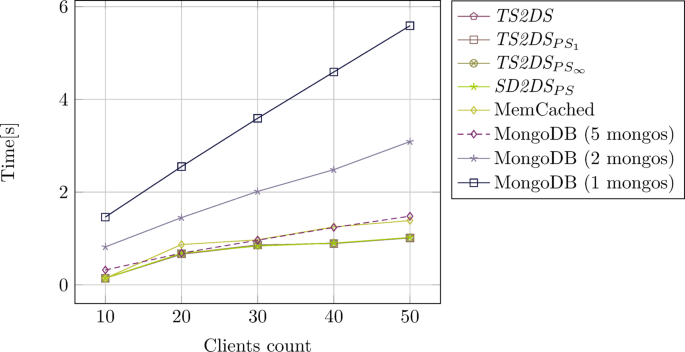
The results for different component sizes (1 MiB, and 10 MiB) are shown in Figs. 4 and 5, respectively. For high-throughput architectures, it was ensured that no copy of the component body existed at the beginning of each test. Copies of all bodies were created while the test was running. (textit{TRESHOLD}) value has been set to 5. The actual value of the (textit{TRESHOLD}) was set arbitrarily since this parameter does not have any impact on consistency issues. This evaluation allows us to properly assess the impact of more than one copy of the body.

According to the analysis of Figures 4 and 5, the longer processing time was obtained for the situation when the value of (C_u) increases in relation to the value of (C_r). Significantly longer query execution times in the case of architecture with increased throughput are caused by the need to update component bodies in two locations. This overhead is a natural consequence of ensuring strong consistency and cannot be bypassed without weakening the consistency model. As the number of clients that modify components decreases, the time approaching the query execution times of the classic version of the architecture. Some fluctuations can be seen, especially in the figure 5, because of the randomnesses in selecting keys of the components to access.

Access time for components of 1MiB.

Full size image

Access time for components of 10MiB.

Full size image

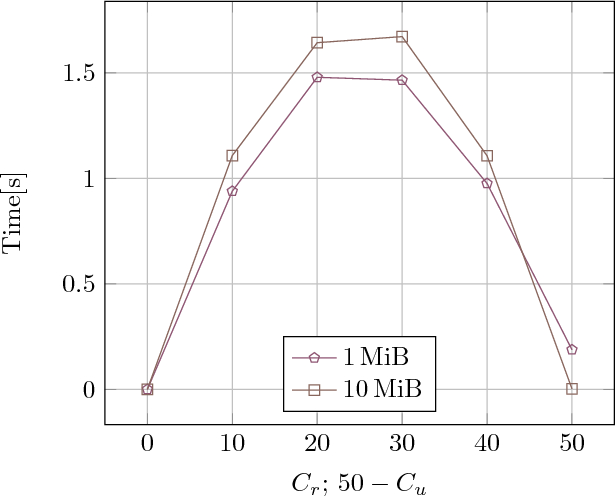
Figure 6 shows how many retrieval queries were rejected during the above experiments for the (textit{TS2DS}_{textit{PS}_1}) architecture. No rejections occurred when only read or modified queries were received. Most of the rejected queries started when the read queries were performed along with the modified queries.

Rejected requests.

Full size image

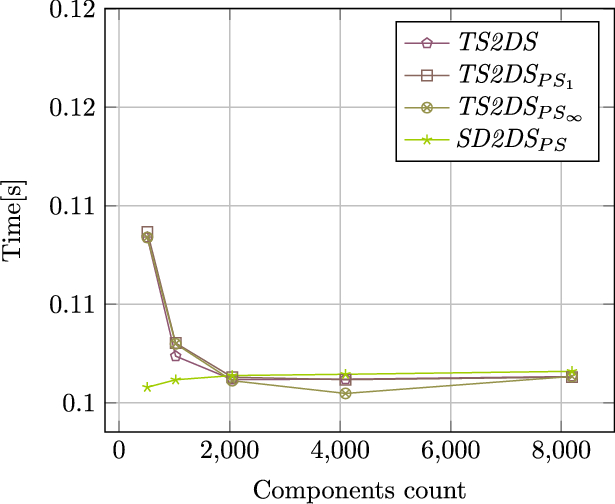
One of the key features of SD2DS is its scalability. Figure 7 shows the downloading times of components depending on the number of buckets and the total number of components in SD2DS. The experiments were carried out in such a way that additional buckets were added when all the buckets used so far contained 512 components.

Scalability comparison while getting components of 10MiB.

Full size image

As can be seen in the analysis of the Fig. 7, the constant increase in the number of components in TS2DS with consistency and the increase in the number of buckets have no effect on the execution time of the primary operations.

In order to reliably evaluate the performance, the prepared implementations were also compared with well-known representations of the NoSQL ecosystem. Two popular systems were selected for comparison: MongoDB and MemCached. All of them were written in C++, as well as our TS2DS. All of them also allow you to work in a distributed environment. MemCached is a system that allows you to cache data in the main memory. MongoDB stores data in non-volatile memory, but it also uses main memory. Like most of the NoSQL systems, both MongoDB and MemCached are usually used to store relatively small data items. Because MongoDB is designed to store documents, it turned out to be necessary to use an additional API (GridFS), which allows you to store larger portions of data with an undefined structure.

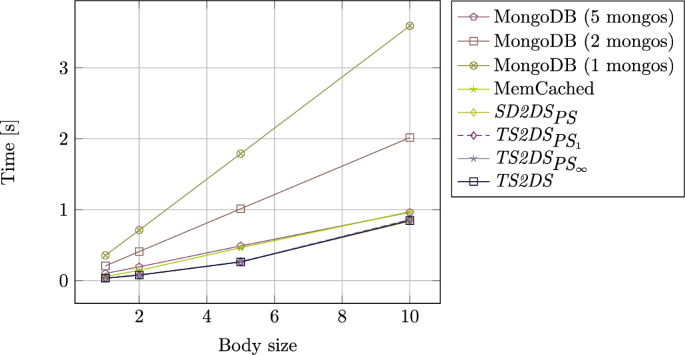
For the benchmark, MemCached and MongoDB were configured in the same way as SD2DS structures. Both MongoDB and MemCached were distributed across 16 servers. However, MongoDB requires additional components to work. A configuration server is located on a separate server. Configuration server plays the similar role to TS2DS coordinator. In addition, MongoDB requires special components (mongos) to run, which allow the addressing servers. Tests were carried out for one, two, and five mongos elements. Each mongos was located on a separate server. MongoDB did not use replicas in the test environment. For TS2DS architectures, efficiency were measured when all components consists of two copies of body. This means that there was an additional copy of the body for each component during the experiments. Figures 8 and 9 present the results of efficiency comparison for components of size 1 MiB and 10 MiB, respectively.

Efficiency comparison while getting components of 1MiB.

Full size image

Efficiency comparison while getting components of 10MiB.

Full size image

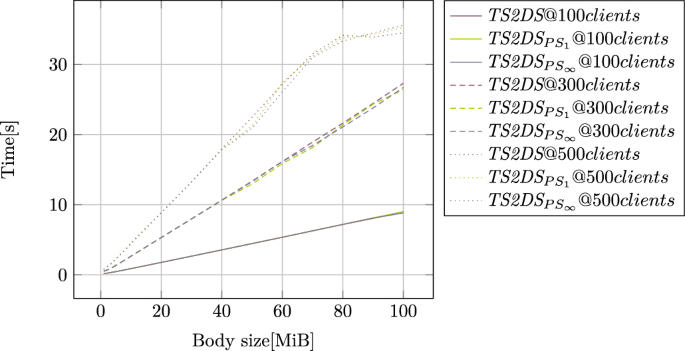
Figures 8 and 9 show similar trends. With increasing workload, processing time also increases. However, the growth for TS2DS architectures is much smaller than for the systems compared. All the architectures of TS2DS and SD2DS show very similar results. The MemCached is optimized for relatively small components³⁹. That is why storing huge data blocks becomes challenging. On the other hand, the efficiency of MongoDB is mostly dependent on the workload of mongos. Since all requests must be passed through those elements, it is very hard to obtain high throughput without a lot of them. This trend can also be seen in the case of a comparison with the relation to the body size of the component as depicted in Figure 10.

Efficiency comparison in relation to component body size.

Full size image

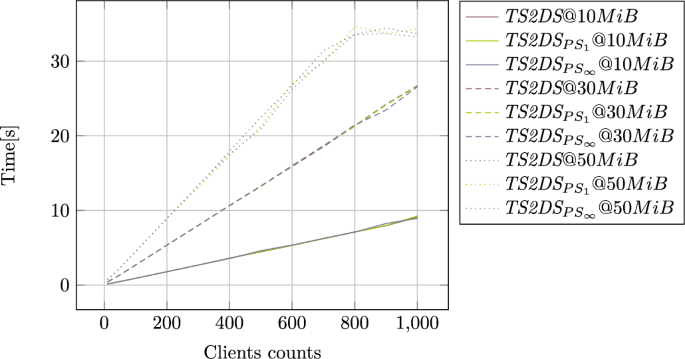
The stress tests performed are presented in Figs. 11 and 12. We used up to 1000 clients that retrieve the components from the structure and components sizes that range between 10MiB and 100MiB. The most interesting fact is that the relations between access times and both the number of clients and component sizes are linear. This also indicates the capability of TS2DS to scale both in therms of component sizes and number of clients that simultaneously operating on the data. It is also worth noting that the access times are almost the same for base architecture and architectures that provide consistency. Because only two copies were used in the TS2DS, the impact of additional copies is not visible when using a large number of clients.

The only exceptions can be seen for very large components accessed by a large number of clients. In those tests, the number of clients that operate in single buckets exceeds the limit of open connection, so they were forced to close by the operating system. Since those situations occur only with really big traffic, it should not be the issue in the real applications. In such a case it is a clear signal to perform additional bucket split to balance the workload.

Relation between the access time and the number of clients during the stress tests.

Full size image

Relation between the access time and the component body sizes during the stress tests.

Full size image

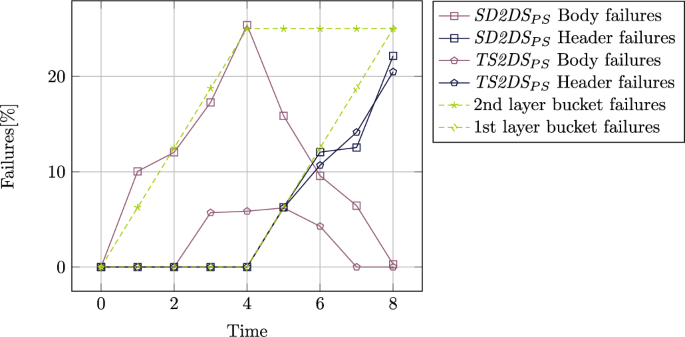
We performed experiments to asses the impact of buckets failures to asses its impact the availability of the components in TS2DS and SD2DS architectures. We introduced failures up to the 25% of all first and second layer buckets in subsequent periods of time while retrieving components from data store. Next, we calculated how many operations failed to execute as a result of failures in retrieving headers or buckets. The results are presented in figure 13. As it can be seen, the TS2DS architecture have serious impact of failures in retrieving bodies from the data store. It is caused by the fact that even with the failure it is still possible to retrieve the component body from second location. Since it is not possible to access the component body when the header is unavailable there is a decrease of the number of body failures while header failures increases. However, introducing second copy of the body do not have any impact on failures during retrieving headers.

Headers and bodies unavailability during bucket failures.

Full size image

In this paper, we proposed a novel NoSQL architecture that is based on Scalable Distributed Two-Layer Data Structures that provide strong consistency along with the increased throughput. We analyzed the impact of increasing throughput in SD2DS and identified inconsistencies during concurrent execution of primary operations and during unfinished primary operations. We identified all inconsistencies of the following categories: Mismatch Body Inconsistency (MBI), Duplicated Body Inconsistency (DBI), Deleted Component Inconsistency (DCI), Orphan Header Inconsistency (OHI), Orphan Body Inconsistency (OBI).

We developed algorithms that allow us to eliminate all the identified inconsistencies and proved their correctness. We experimentally evaluated the performance of our consistent data store in relation to the known NoSQL representatives like MongoDB and MemCached. Comparative tests with the MongoDB and MemCached systems have shown that the prepared data store can successfully compete with publicly available solutions. This makes it possible to use the SD2DS system in practical IT systems that require high performance and consistency.

Experimental results show that the introduction of replication can seriously increase performance and throughput. This conclusion is especially true in the cases where component modifications are not frequent. On the other hand, ensuring consistency in the cases of frequent modifications may seriously impact performance. This is perfectly natural, as it must be ensured that all copies are modified at the same time to ensure consistency. In addition, introducing replicas is always related to the additional costs of storage space and latency caused by the replication. In the case of the TS2DS it is possible to reduce this cost by replicating only those components that are frequently read. Modification of the replication threshold allows for an additional method of fine-tuning the trade-off between performance and storage cost.

Future work is oriented toward the further development of this architecture to create a fully scalable data store that allows for efficient data processing.